The average velocity gained by the free electrons of a conductor in the opposite direction of the externally applied electric field is called Drift Velocity. The parameter ![]() is called drift velocity of electrons.
is called drift velocity of electrons.
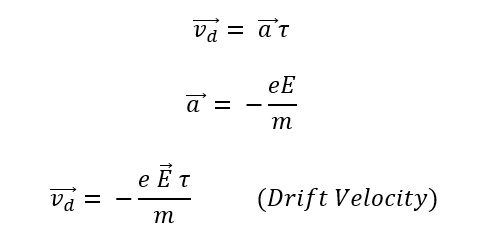
The relation between Electric current and Drift velocity:
Derivation of OHM’S Law:
Current in terms of drift velocity (vd) is I = enAvd
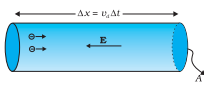
Number of electrons in length l of the conductor = n × volume of the conductor = n Al
Total charge contained in length l of the conductor is q = en Al
All the electrons which enter the conductor at the right end will pass through the conductor at the left end in time,
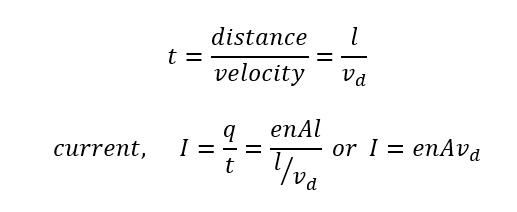
This equation relates the current I with the drift velocity vd
Current density ‘j’ is given by
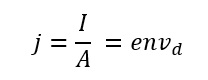
In vector form,
![]()
The above equation is valid for both positive and negative values of q.
Deduction of Ohm’s Law:
when a potential difference V is applied across a conductor of length l, the drift velocity in terms of V is given by
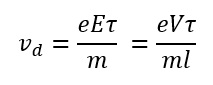
If the area of cross section of the conductor is A and the number of electrons per unit volume of the electron density of the conductor is n, then the current through the conductor will be
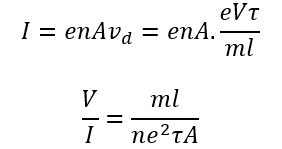
At a fixed temperature, the quantities m, l, n, e, τ and A, all have constant values for a given conductor.
Therefore,

This prove Ohm’s law for a conductor and here
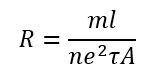
is the resistance of the conductor.
Resistivity in terms of electron density and relaxation time:
The resistance R of a conductor of length l, the area of cross-section A and resistivity ρ is given by
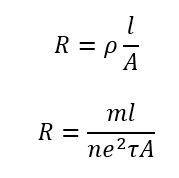
where τ is the relaxation time. Comparing the above two equations, we get
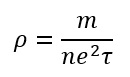
Constant value e = 1.6 × 10-19C.
Obviously, ρ is independent of the dimension of the conductor but depends on its two parameters:
- The number of free electrons per unit volume or electron density of the conductor.
- The relaxation time τ, the average time between two successive collisions of an electron.
Units:
Drift velocity vd is in ms-1 , free-electron density in m3, cross-sectional area A in m2, current density j in Am-2. All resistance in Ω.

