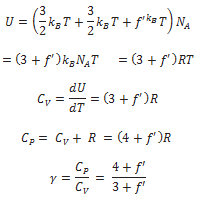Specific Heat Capacity
- Monatomic Gases
- Diatomic Gases
- Polyatomic Gases
Specific Heats of Monatomic Gases:
The molecule of a monatomic gas has only three translational degrees of freedom.
Thus, the average energy of a molecule at temperature T is
![]()
The total internal energy of a mole of such a gas is
![]()
The molar specific heat at constant volume, Cv is
![]()
For an ideal gas,
![]()
where Cp is the molar specific heat at constant pressure. Thus,
![]()
The ratio of specific heats
![]()
Specific Heats of Diatomic Gases:
A diatomic molecule treated as a rigid rotator like a dumbbell has 5 degrees of freedom: 3 translational and 2 rotational. Using the law of equipartition of energy, the total internal energy of a mole of such a gas is
![]()
The molar specific heats are then given by
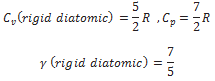
If the diatomic molecule is not rigid but has, in addition, a vibration mode

Specific Heats of Polyatomic Gases:
A polyatomic molecule has 3 translational, 3 rotational degrees of freedom and a certain number (f) of vibration modes. According to the law of equipartition of energy, it is easily seen that one mole of such a gas has