The total mechanical energy of a system is conserved if the forces, doing work on it, are conservative.
Suppose that a body undergoes displacement Δx under the action of a conservative force F. Then from the WE theorem we have,
![]()
If the force is conservative, the potential energy function V(x) can be defined such that
![]()
The above equations imply that which means that K + V, the sum of the kinetic and potential energies of the body is constant.
![]()
Over the whole path, xi to xf, this means that
![]()
The quantity K +V(x), is called the total mechanical energy of the system. Individually the kinetic energy K and the potential energy V(x) may vary from point to point, but the sum is a constant.

The total mechanical energies E0, Eh, and EH of the ball at the indicated heights zero (ground level), h and H, are
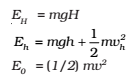
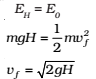
a result that was obtained for a freely falling body.
Further,
![]()
which implies,
![]()
and is a familiar result from kinematics.
At the height H, the energy is purely potential. It is partially covered to kinetic at height h and is fully kinetic at ground level. This illustrates the conservation of mechanical energy.

