Energy possessed by the spring by virtue of compression or expansion against elastic force in the spring is known as elastic potential energy or Potential energy of a spring.
Spring:
It is a coiled structure made up of elastic material & is capable of applying restoring force & restoring torque when disturbed from its original state. When a force (F) is applied at one end of the string, parallel to its length, keeping the other end fixed, then the spring expands (or contracts) & develops a restoring force (FR) which balances the applied force in equilibrium.
On increasing, applied force spring further expands in order to increase restoring force for balancing the applied force. Thus restoring force developed within the spring is directed proportional to the extension produced in the spring.
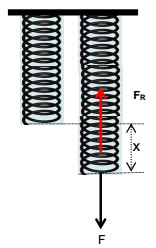

Case 1: If x = 1, FR = k, Hence force constant of the string may be defined as the restoring force developed within spring when its length is changed by unity.
But in equilibrium, restoring force balances applied force.
F = FR = k x
Case 2: If x = 1, F = 1, Hence force constant of the string may also be defined as the force required to change its length by unity in equilibrium.
Mathematical Expression for Elastic Potential Energy
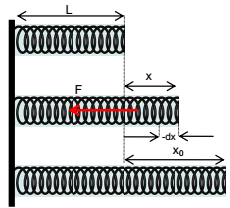
Consider a spring of natural length ‘L’ & spring constant ‘k’ its length is increased by x0. The elastic potential energy of stretched spring will be equal to total work done by the spring in regaining its original length.
If in the process of regaining its natural length, at any instant extension in the spring was x then force applied by spring is
F = k x
If spring normalizes its length by elementary distance dx opposite to x under this force then work done by spring is
![]()
(force applied by spring F and displacement –dx has taken opposite to extension x are in the same direction)
![]()
Total work done by the spring in regaining its original length is obtained by integrating dW from x0 to 0
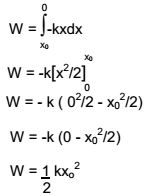
This work was stored in the body in the form of elastic potential energy.
![]()

