Energy stored in a capacitor
The energy U stored in a capacitor of capacitance C, with charge Q and voltage V is
The electric energy density (energy per unit volume) in a region with electric field is (1/2)ε
Explain in detail:
Consider a capacitor of capacitance C, completely uncharged in the beginning. Charging process of capacitor requires the expenditure of energy because while charging a capacitor charge is transferred from the plate at lower potential to plate at higher potential. Now if we start charging the capacitor by transporting a charge dQ from negative plate ti the positive plate then work is done against the potential difference across the plate. If q is the amount of charge on the capacitor at any stage of charging process and φ is the potential difference across the plates of capacitor then magnitude of the potential difference is φ=q/C. Now work dW required to transfer dq is
![]()
To charge the capacitor starting from the uncharged state to some final charge Q work required is Integrating from 0 to Q
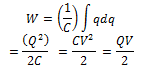
which is the energy stored in the capacitor and can also be written as
![]()
we see that the total work done is equal to the average potential V/2 during the charging process, multiplied by the total charge transferred. If C is measured in Farads, Q in coulombs and V in volts the energy stored would in Joules. A parallel plate capacitor of area A and separation d has capacitance
![]()
Electric field in the space between the plates is
![]()
Putting above values of V and C
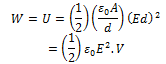
If u denotes the energy per unit volume or energy density then
![]()
The result for above equation is generally valid even for the electrostatic field that is not constant in space.

