Kinematic Equations of Motion

For objects in uniformly accelerated rectilinear motion, the five quantities, displacement x, the time took t, initial velocity v₀, final velocity v and acceleration a are related by a set of simple equations called kinematic equations of motion :

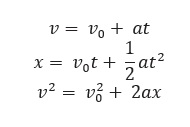
if the position of the object at time t = 0 is 0. If the particle starts at x = x₀ , x in above equations is replaced by (x- x₀).

Kinematical Graphs

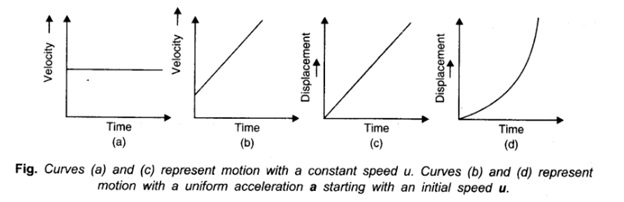
The ‘displacement-time’ and the ‘velocity-time’ graphs of a particle are often used to provide us with a visual representation of the motion of a particle. The ‘shape’ of the graphs depends on the initial ‘co-ordinates’ and the ‘nature’ of the acceleration of the particle (Fig.)

Equations of Uniformly Accelerated Motion

If a body starts with velocity (u) and after time t its velocity changes to v, if the uniform acceleration is a and the distance traveled in time t in s, then the following relations are obtained, which are called equations of uniformly accelerated motion.

1. v = u + at
2. s = ut + at²
3. v² = u² + 2as

Distance traveled in nth second

If a body moves with uniform acceleration and velocity changes from u to v in a time interval, then the velocity at the midpoint of its path

√u² + v²/ 2

Motion under Gravity

If an object is falling freely (u = 0) under gravity, then equations of motion

1. v = u + gt
2. h =ut +gt²
3. v² = u² + 2gh

Note: If an object is thrown upward then g is replaced by – g in above three equations. It thus follows that

Time is taken to reach maximum height:

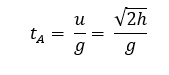Maximum height reached by the body:

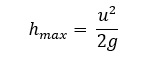
A ball is dropped from a building of height h and it reaches after t seconds on earth. From the same building if two balls are thrown (one upwards and other downwards) with the same velocity u and they reach the earth surface after t, and t₂ seconds respectively, then

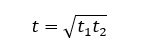
When a body is dropped freely from the top of the tower and another body is projected horizontally from the same point, both will reach the ground at the same time.