When a charged capacitor is allowed to discharge through a non-resistance, electrical oscillations of constant amplitude and frequency are produced. These oscillations are called LC-oscillations.
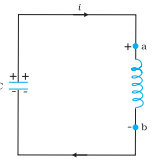
Fig. At the instant shown, the current
is increasing so the polarity of induced emf in the inductor is as shown
Let a capacitor be charged qm (at t = 0) and connected to an inductor as shown in Fig.
The moment the circuit is completed, the charge on the capacitor starts decreasing, giving rise to the current in the circuit. Let q and i be the charge and current in the circuit at time t. Since di/dt is positive, the induced emf in L will have polarity as shown, i.e., vb < va . According to Kirchhoff’s loop rule,
i = -(dq/dt) in the present case (as q decreases, I increases).
This equation has the form for
a simple harmonic oscillator. The charge, therefore, oscillates with a natural frequency.
And varies sinusoidally with time as
where qm is the maximum value of q and φ is a phase constant. Since q = qm at t = 0, we have cos ϕ =1 or φ = 0. Therefore, in the present case
The current i(= -dq/dt) is given by
Figure (a) shows a capacitor with initial charge qm connected to an ideal inductor. The electrical energy stored in the charged capacitor is
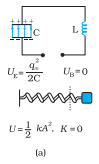
.Since, there is no current in the circuit; energy in the inductor is zero. Thus, the total energy of LC circuit is
