Young’s Double Slit Experiment (YDSE)

Young’s Double Slit Experiment (YDSE)

Monochromatic light (single wavelength) falls on two narrow slits S₁ and S₂ which are very close together acts as two coherent sources when waves coming from two coherent sources (S₁, S₂ ) superimposes on each other, an interference pattern is obtained on the screen. In YDSE alternate bright and dark bands obtained on the screen. These bands are called Fringes.

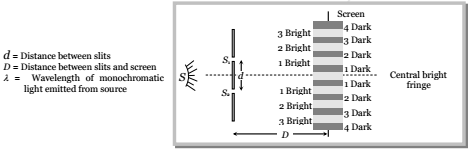
1. Central fringe is always bright, because at central position 0⁰ or 0
2. The fringe pattern obtained due to a slit is brighter than that due to a point.
3. If the slit widths are unequal, the minima will not be complete dark. For very large width uniform illumination occurs.
4. If one slit is illuminated with red light and the other slit is illuminated with blue light, no interference pattern is observed on the screen.
5. If the two coherent sources consist of object and it’s reflected image, the central fringe is dark instead of bright one.
6. Path difference: Path difference between the interfering waves meeting at a point P on the screen is given by

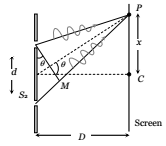
where x is the position of point P from central maxima.
For maxima at P: n ; where n = 0, 1, 2,…..

and For minima at P:

where n = 1, 2, …….

Note: If the slits are vertical, the path difference () is d sin , so as increases, also increases. But if slits are horizontal path difference is d cosθ , so as increases, decreases.

More about fringe

All fringes are of equal width. Width of each fringe is:

and angular fringe width:

• If the whole YDSE set up is taken in another medium then changes so changes e.g. in water

• Fringe width β ∝ 1/d i.e. with increase in separation between the sources, decreases.
• Position of n^th bright fringe from central maxima

• Position of n^th dark fringe from central maxima

• In YDSE, if n₁ fringes are visible in a field of view with light of wavelength ₁ , while n₂ with light of wavelength ₂ in the same field, then n₁₁ n_{2 2} .
• Separation (x) between fringes

Identification of central bright fringe

To identify central bright fringe, monochromatic light is replaced by white light. Due to overlapping central maxima will be white with red edges. On the other side of it we shall get a few colored band and then uniform illumination.

Condition for observing sustained interference

• The initial phase difference between the interfering waves must remain constant: Otherwise the interference will not be sustained.
• The frequency and wavelengths of two waves should be equal: If not the phase difference will not remain constant and so the interference will not be sustained.
• The light must be monochromatic: This eliminates overlapping of patterns as each wavelength
  corresponds to one interference pattern.
• The amplitudes of the waves must be equal: This improves contrast with I_max = 4I₀ and I_min 0.
• The sources must be close to each other: Otherwise due to small fringe width ( β ∝ 1/d )the eye cannot resolve fringes resulting in uniform illumination.

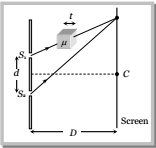
Shifting of fringe pattern in YDSE

If a transparent thin film of mica or glass is put in the path of one of the waves, then the whole fringe pattern gets shifted.
If film is put in the path of upper wave, fringe pattern shifts upward and if film is placed in the path of lower wave, pattern shift downward.

• Additional path difference = (μ – 1)t
• If shift is equivalent to n fringes then

• Shift is independent of the order of fringe (i.e. shift of zero order maxima = shift of n^th order maxima.
• Shift is independent of wavelength.