
A liquid air interface has energy, so for a given volume, the surface with minimum energy is the one with the least area. The sphere has this property.
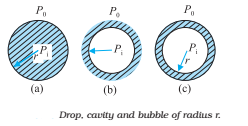
Another interesting consequence of surface tension is that the pressure inside a spherical drop Fig. (a) is more than the pressure outside. Suppose a spherical drop of radius r is in equilibrium. If its radius increased by Δr. The
extra surface energy is
![]()
If the drop is in equilibrium this energy cost is balanced by the energy gain due to expansion under the pressure difference (Pi – Po) between the inside of the bubble and the outside. The work done is
![]()
So that
![]()
In general, for a liquid-gas interface, the convex side has a higher pressure than the concave side. For example, an air bubble in a liquid would have a higher pressure inside it. See Fig (b).
A bubble Fig (c) differs from a drop and a cavity; in this, it has two interfaces. Applying the above argument we have for a bubble
![]()
This is probably why you have to blow hard, but not too hard, to form a soap bubble. A little extra air pressure is needed inside!

