Equipotential surfaces
- Surface over which the electric potential is same everywhere is called an equipotential surface.
- Equipotential surfaces are the graphical way to represent potential distribution in an electric field.
- We can draw equipotential surfaces through a space having the electric field.
- For a positive charge, the electric field would be in radially outward direction and the equipotential surfaces would be concentric spheres with centers at the charge as shown below in the figure.
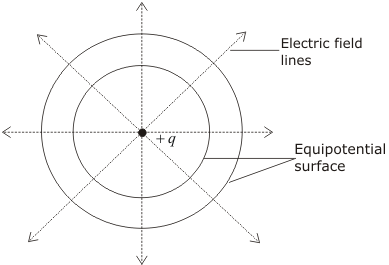
- Since electric potential remains same everywhere on an equipotential surface from this it follows that PE of a charged body is same at all points on this surface. This shows that work done in moving a charged body between two points on an equipotential surface would be zero.
- At every point on the equipotential surface, electric field lines are perpendicular to the surface. This is because potential gradient along any direction parallel to the surface is zero i.e.,
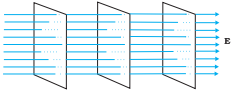
so component electric parallel to the equipotential surface is zero. - For a uniform electric field E, say, along with the x-axis, the equipotential surfaces are planes normal to the x-axis, i.e., planes parallel to the y-z plane.
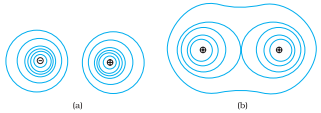
Equipotential surfaces for (a) a dipole and (b) two identical positive charges
Electric Potential Energy
Potential energy
The potential energy stored in a system of charges is the work done (by an external agency) in assembling the charges at their locations. The potential energy of two charges q1, q2 at r1, r2 is given by
where r12 is the distance between q1 and q2.
The potential energy of a charge q in an external potential V(r) is qV(r). The potential energy of a dipole moment p in a uniform electric field E is –p.E.
Electric Potential Energy
Consider an electrostatic field E due to a charge Q placed at the origin. Now, bring a test charge q from a point R to a point P against the repulsive force on it due to the charge Q. This will happen if Q and q are either positive or both negative.
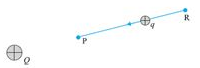
Work done by external forces in moving a charge q from R to P is
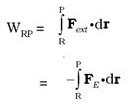
At every point in the electric field, a particle with charge q possesses a certain electrostatic potential energy, this work done increases its potential energy by an amount equal to the potential energy difference between points R and P.
Thus, potential energy difference
![]()
(Note here that this displacement is in an opposite sense to the electric force and hence work done by electric field is negative, i.e., –WRP.)
Therefore, can define electric potential energy difference between two points as the work required to be done by an external force in moving (without accelerating) charge q from one point to another for the electric field of any arbitrary charge configuration.
Two important comments may be made at this stage:
- Work done by an electrostatic field in moving a charge from one point to another depends only on the initial and the final points and is independent of the path taken to go from one point to the other. This is the fundamental characteristic of a conservative force.
![]()
- A convenient choice is to have electrostatic potential energy zero at infinity. With this choice, if take the point R at infinity,
![]()
The potential energy of charge q at a point (in the presence of field due to any charge configuration) is the work done by the external force (equal and opposite to the electric force) in bringing the charge q from infinity to that point.

