Force:

A force is necessary to keep a body in uniform motion is wrong. A force is necessary for the practice to counter the opposing force of friction.

The SI unit of force is Newton: 1 N = 1 kg m s^-2.

1. The second law is consistent with the First Law (F = 0 implies a = 0)
2. It is a vector equation
3. It is applicable to a particle, and also to a body or a system of particles, provided F is the total external force on the system and a is the acceleration of the system as a whole.
4. F at a point at a certain instant determines a at the same point at that instant. That is the Second Law is a local law; a at an instant does not depend on the history of motion.

Newton’s Law

Newton’s First Law

Galileo extrapolated simple observations on motion of bodies on inclined planes and arrived at the law of inertia. Newton’s first law of motion is the same law rephrased thus: “Everybody continues to be in its state of rest or of uniform motion in a straight line, unless compelled by some external force to act otherwise”. In simple terms, the First Law is “If external force on a body is zero, its acceleration is zero”

When there is no net force on an object at rest remains at rest, and an object in motion continues to move with a velocity that is constant in magnitude and direction.

Note:

1. Newton’s first law really describes a reference frame. The property of the body to remain at rest or to retain its uniform linear motion in the absence of applied force is called Inertia.
   The first law is often called the law of intertie and the reference frames to which it applies are termed as inertial reference frames. Thus an inertial reference frame is one which is either at rest or moves with a constant velocity relative to earth. Truly speaking, the earth itself is not an inertial reference frame (because it rotates as well as moves around the sun in an orbit) but for most practical purposes we can treat it as an inertial reference frame. Greater the mass of the body greater is the inertia. That is mass is the measure of the inertia of the body
2. This law does not differentiate between objects at rest and objects moving with constant velocity. Indeed, an object moving with constant velocity in one inertial reference frame can be at rest in another inertial reference frame.
3. No net force here may mean the absence of all forces or the presence of forces whose resultant is zero.

Newton’s Second Law

We know from the first law, what happens when there is no unbalanced force on an object: its velocity remains constant. Now let us see what happens when there is no unbalanced force on an object? The Newton’s second law gives an answer to this question, that is, the net force acting on a body will produce acceleration.

When there is a constant unbalanced force on an object, the object moves with constant acceleration. Furthermore, if the force varies, the acceleration varies in direct proportion with larger force producing larger acceleration. Twice the force products twice the acceleration of the same mass.

The magnitude of the acceleration produced depends on the quantity of matter being pushed. The quantity of matter is referred to as the inertial mass.

The rate of change of momentum of a body is proportional to the applied force and takes place in the direction in which the force acts. Thus

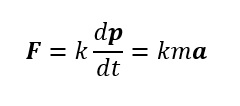
Where F is the net external force on the body and a its acceleration. We set the constant of proportionality k = 1 in S.I. Then

Newton’s second law states the relationship between the net force and the inertial mass.

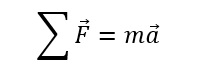
Note: that the direction of acceleration is in the direction of the net forced. In terms of component

Momentum:

Momentum, P of a body is defined to be the product of its mass m and velocity v, and is denoted by P. Momentum is clearly a vector quantity.

P = m v

Impulse:

Impulse is the product of force and time which equals the change in momentum.

Impulse = Force × time duration = change in momentum

The notion of impulse is useful when a large force acts for a short time to produce a measurable change in momentum. Since the time of action of the force is very short, one can assume that there is no appreciable change in the position of the body during the action of the impulsive force.

Newton’s Third Law

Experiments show that forces occur in pairs. If you push against a wall, the wall pushes back at you. If on body A applies a force F_AB on another body B, body B applies an equal but oppositely directed force F_BA on A i.e.

Normally, one of these force (it does not matter which) is called the action force and the other is called the reaction force. Thus the third law is also sometimes stated as “To every action there is always an equal and opposite reaction”. Note that the action and reaction always act on different objects.

Let us note some important points about the third law, particularly in regard to the usage of the terms: action and reaction:

1. Forces always occur in pairs. Force on a body A by B is equal and opposite to the force on the body B by A.
2. There is no cause effect relation implied in the third law. The force on A by B and the force on B by A act
   at the same instant.
3. Action and reaction forces act on different bodies, not on the same body. Consider a pair of bodies A and B. According to the third law,

(force on A by B) = – (force on B by A)

Thus if we are considering the motion of any one body (A or B), only one of the two forces is relevant. It is an error to add up the two forces and claims that the net force is zero.