The inertia of rotational motion is called the moment of inertia. It is denoted by L.
Moment of inertia is the property of an object by virtue of which it opposes any change in its state of rotation about an axis.
The moment of inertia of a body about a given axis is equal to the sum of the products of the masses of its constituent particles and the square of their respective distances from the axis of rotation.

Moment of inertia of a body

Its unit is kg.m2 and its dimensional formula is [ML2].
The moment of inertia of a body depends upon
- position of the axis of rotation
- orientation of the axis of rotation
- shape and size of the body
- distribution of mass of the body about the axis of rotation.
- The physical significance of the moment of inertia is same in rotational motion as the mass in linear motion.
The Radius of Gyration
The root mean square distance of its constituent particles from the axis of rotation is called the radius of gyration of a body. It is denoted by K.
Radius of gyration
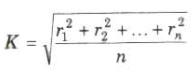
The product of the mass of the body (M) and square of its radius gyration (K) gives the same moment of inertia of the body about rotational axis.
Therefore, moment of inertia I = MK2 ⇒ K = √1/M
Parallel Axes Theorem
The moment of inertia of any object about any arbitrary axes is equal to the sum of moment of inertia about a parallel axis passing through the centre of mass and the product of mass of the body and the square of the perpendicular distance between the two axes.

Mathematically I = ICM + Mr2
where I is the moment of inertia about the arbitrary axis, ICM is the moment of inertia about the parallel axis through the centre of mass, M is the total mass of the object and r is the perpendicular distance between the axis.
Perpendicular Axes Theorem
The moment of inertia of any two-dimensional body about an axis perpendicular to its plane (IZ) is equal to the sum of moments of inertia of the body about two mutually perpendicular axes lying in its own plane and intersecting each other at a point, where the perpendicular axis passes through it.

Mathematically IZ = IX + IY
where IX and IY are the moments of inertia of plane lamina about perpendicular axes X and Y respectively which lie in the plane lamina an intersect each other.
Theorem of parallel axes is applicable for any type of rigid body whether it is a two dimensional or three dimensional, while the theorem of perpendicular is applicable for the laminar type or two I dimensional bodies only.

