The resultant torque acting on the body must be zero. The sum of anti-clockwise torques about any axis must be equal to the sum of clockwise torques about the same axis.
The means the algebraic sum of all the torques acting on the body about the axis of rotation must be zero.
The general conditions of equilibrium are
- The algebraic sum of the resolved components of the forces in any fixed direction must be zero.
- The algebraic sum of the resolved components of the forces in a perpendicular direction must be zero.
- The algebraic sum of the torques or moments of the forces about any point in their plane must be zero.
Centre of Gravity
The centre of gravity of an extended body is that point where the total gravitational torque on the body is zero.
Take an irregularly shaped cardboard and a narrow tipped object like a pencil. You can locate by trial and error a point G on the cardboard where it can be balanced on the tip of the pencil. (The cardboard remains horizontal in this position.) This point of balance is the centre of gravity (CG) of the cardboard.
The tip of the pencil provides a vertically upward force due to which the cardboard is in mechanical equilibrium.
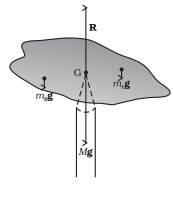
Balancing a cardboard on the tip of a pencil. The point of support, G, is the centre of gravity.
In fig, the reaction of the tip is equal and opposite to Mg, the total weight of (i.e., the force of gravity on) the cardboard and hence the cardboard is in translational equilibrium. It is also in rotational equilibrium; if it were not so, due to the unbalanced torque it would tilt and fall. There are torques on the card board due to the forces of gravity like m1g, m2g …. etc, acting on the individual particles that make up the cardboard.
If ri is the position vector of the ith particle of an extended body with respect to its CG, then the torque about the CG, due to the force of gravity on the particle is τ = ri × mig. The total gravitational torque about the CG is zero, i.e.
![]()
We may, therefore, define the CG of a body as that point where the total gravitational torque on the body is zero.

