Whenever there is a change in the magnetic flux linked with a coil, there is also a change of flux linked with the neighbouring coil, producing an induced emf in the second coil. This phenomenon of producing an induced emf in a coil due to the change in current in the other coil is known as mutual induction.
The coefficient of mutual induction:
At any instant, Magnetic flux linked with the secondary coil α current in the primary coil
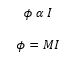
where M is mutual inductance or coefficient of mutual induction of the two coils.
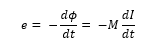
Case1: If I = 1 , then ϕ = M
Thus the mutual inductance of two coil is numerically equal to the magnetic flux linked with one coil when a unit current passes through the other coil.
Case 2: If dI/dt = 1, then e = -M
Thus the mutual inductance of a coil may be defined as the induced emf set up in one coil when the current in the neighboring coil changes at the unit rate.
Unit of mutual inductance: 1henry (H)
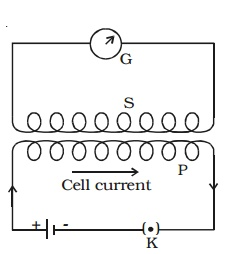
Mutual inductance of two long solenoids:
S1 and S2 are two long solenoids each of length l. The solenoid S2 is wound closely over the solenoid S1 (Fig 4.8).

N1 and N2 are the number of turns in the solenoids S1 and S2 respectively. Both the solenoids are considered to have the same area of cross section A as they are closely wound together. I1 is the current flowing through the solenoid S1. The magnetic field B1 produced at any point inside the solenoid S1 due to the current I1 is
![]()
The magnetic flux linked with each turn of S2 is equal to B1 A.
Total magnetic flux linked with solenoid S2 having N2 turns is
![]()
Substituting for B1 from equation (1)
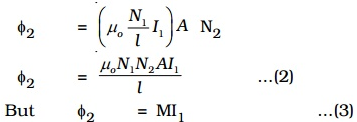
where M is the coefficient of mutual induction between S1 and S2.
From equations (2) and (3)
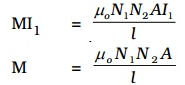
If the core is filled with a magnetic material of permeability μ.
![]()

