
Refraction by Spherical Surfaces:
A refracting surface is the part of a sphere separating two transparent media.
The spherical refracting surfaces are of two types:
- Convex spherical refracting surface
- Concave spherical refracting surface
For any curved surface area,
![]()
This is the relation between object and image distance in terms of the refractive index of the medium and the radius of curvature of the curved spherical surface.
Refraction by Lenses and Lens Maker’s Formula:
A lens is a homogeneous transparent medium bounded by two curved surfaced or one curved an one plane surface. The curved surface may be spherical, cylindrical or paraboloidal; but most of the surfaces are spherical.
The most common Lens maker’s formula is:
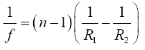
The Gaussian form of lens equation or the thin lens formula is:
![]()
From the Lens Maker’s formula, it is clear that for refraction of light through a lens that the focal length f also depends upon the radii of curvature R1 and R2 of its surfaces. For a double convex lens, R1 is positive and R2 is negative. This is why; the air bubble (whose surface is convex) behaves as a concave lens inside water.
The linear magnification produced by the spherical lens is the ratio of the size of the image formed by the lens to the size of the object, both measured perpendicular to the principal axis.
Therefore,
![]()
According to the sign convention, for erect (and virtual) image formed by a convex or concave lens, m is positive, while for an inverted (and real) image, m is negative.
Power (P) of a thin lens is equal to the reciprocal of its focal length (f) measured in meter.
![]()
The S.I. Unit for the power of a lens is ‘Dioptre’.
Combination of lenses helps to obtain diverging or converging lenses of desired magnification. It also enhances the sharpness of the image.
The combined focal length of the combination of lens is,
![]()
And their combined magnification is,
![]()

