Stokes’ Law and Terminal velocity

According to Stokes’ law, the backward viscous force acting on a small spherical body of radius r moving with uniform velocity v through fluid of viscosity η is given by

Where, r = Radius of the spherical body

v = velocity of the spherical body

It gives the relationship between retarding force and velocity. When viscous force plus buoyant force becomes equal to force due to gravity, the net force becomes zero. The sphere then descends with a constant terminal velocity (v_t).

Now,

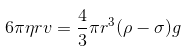
Where, ρ = Density of the liquid

σ = Density of the spherical body

Terminal velocity of a spherical body of density ρ and radius r moving through a liquid of density ρ’ is

where,
ρ = density of body,

σ = density of liquid,

η = coefficient of viscosity of liquid and,

g = acceleration due to gravity

1. If ρ > ρ₀, the body falls downwards.
2. If ρ < ρ₀, the body moves upwards with the constant velocity.
3. If po << ρ, v = (2r²ρg/9η)

Importance of Stokes’ Law

• This law is used in the determination of electronic charge by Millikan in his oil drop
  experiment.
• This law helps a man coming down with the help of a parachute.
• This law account for the formation of clouds.