Heat Capacity

Heat Capacity of a system is defined as the amount of heat required to raise the temperature of a system by 1^oC.

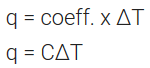
where, coefficient C is called the heat capacity.

C is directly proportional to the amount of substance.

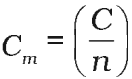
It is the heat capacity for 1 mole of the substance.

Molar heat capacity

It is defined as the quantity of heat required to raise the temperature of a substance by 1^o (kelvin or Celsius).

Specific Heat Capacity

It is defined as the heat required to raise the temperature of one unit mass of a substance by 1^o (kelvin or Celsius).

q = C × m × ∆T

where m = mass of the substance

∆T = rise in temperature.

Relation between C_p and C_v for an Ideal Gas

At constant volume heat capacity = C_v

At constant pressure heat capacity = C_p

At constant volume q_v = C_v ∆T = ∆U

At constant pressure q_v = C_p ∆T = ∆H

For one mole of an ideal gas

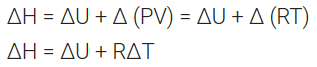
On substituting the values of ∆H and ∆U, the equation is modified as

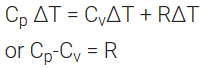
Measurement of ∆U and ∆H: Calorimetry

Determination of ∆U: ∆U is measured in a special type of calorimeter, called bomb calorimeter.

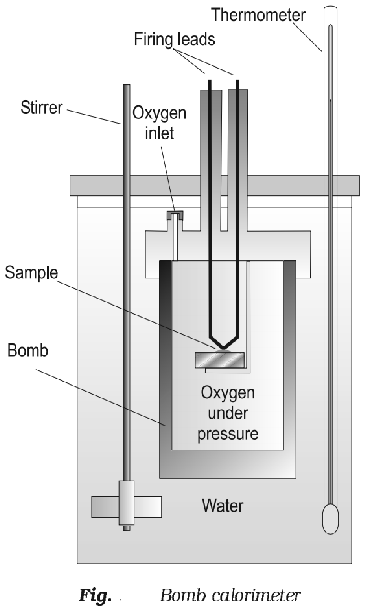
Working with calorimeter:

The calorimeter consists of a strong vessel called (bomb) which can with stand very high pressure. It is surrounded by a water bath to ensure that no heat is lost to the surrounding.

Procedure:

A known mass of the combustible substance is burnt in the pressure of pure dioxygen in the steel bomb. Heat evolved during the reaction is transferred to the water and its temperature is monitored.

During the process volume remains constant

∆V = 0

Temperature change of the calorimeter is converted to q_v.

The value of ∆U can be calculated using the formula.

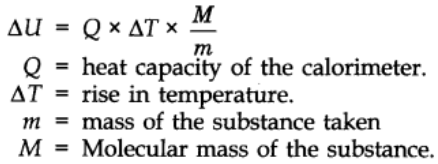
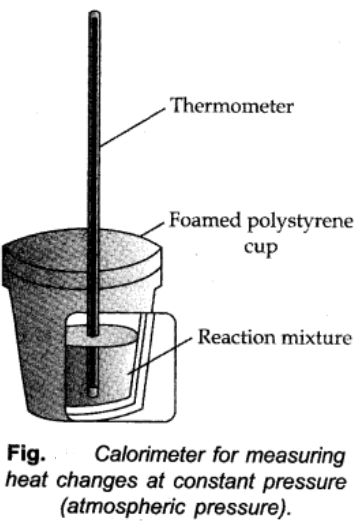
Determination of ∆H:

At constant pressure heat evolved or absorbed is ∆q_p is equal to the heat of reaction or enthalpy of reaction ∆_rH.

∆_rH = (Sum of enthalpies of products) – (Sum of enthalpies of reactants)

a_i and b_i are the stoichiometric coefficients.

Standard enthalpy of reactants: When reaction takes place at the standards state of substance the enthalpy of reaction is known as standard enthalpy. It is denoted by ∆H^⊖.