Oscillations due to a spring:
The simplest observable example of simple harmonic motion is the small oscillations of a block of mass m fixed to a spring, which in turn is fixed to a rigid wall as shown in above Fig.
A system when deformed, is subject to a restoring force, the magnitude of which is proportional to the deformation or the displacement and acts in opposite direction. This is known as Hooke’s law.
It holds good for displacements small in comparison to the length of the spring. At any time t, if the displacement of the block from its mean position is x, the restoring force F acting on the block is,
![]()
The constant of proportionality, k, is called the spring constant, its value is governed by the elastic properties of the spring.
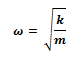
And the period, T, of the oscillator is given by,
![]()
Above two equation tell us that a large angular frequency and hence a small period is associated with a stiff spring (high k) and a light block (small m).

