Simple harmonic motion
In simple harmonic motion (SHM), the displacement x(t) of a particle from its equilibrium position is given by,
![]()

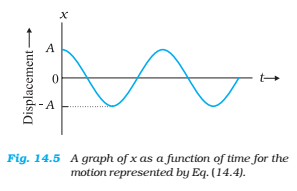
A term that means the periodic motion is a sinusoidal function of time. Equation 3, in which the sinusoidal function is a cosine function, is plotted in Fig. 14.5.
in which A is the amplitude of the displacement, the quantity (ωt + ϕ) is the phase of the motion, and ϕ is the phase constant.
The angular frequency ω is related to the period and frequency of the motion by,
![]()
The SI unit of angular frequency is radians per second.
To illustrate the significance of period T, sinusoidal function with two different periods are plotted in below graph.
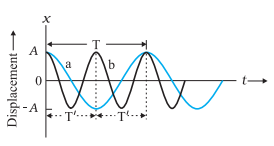
Fig. Plots of Eq. for ? = 0 for two different periods.
In this plot, the SHM represented by curve a, has a period T and that represented by curve b, has a period T’ = T/2.
Simple harmonic motion is the projection of uniform circular motion on a diameter of the circle in which the latter motion takes place.
Velocity and Acceleration in simple Harmonic Motion
The magnitude of velocity, v, with which the reference particle P is moving in a circle is related to its angular speed, ω as
![]()
where A is the radius of the circle describe by the particle P. its projection on the x-axis at any time t, as shown in above Fig. is
![]()
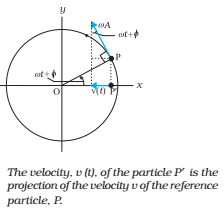
The negative sign appears because the velocity component of P is directed towards the left, in the negative direction of x. Eq. (4) expresses instantaneous velocity of the particle P’ (projection of P). Therefore, it expresses the instantaneous velocity of a particle executing SHM. Eq. (4) can also be obtained by differentiating Eq. (3) w.r.t as,
![]()
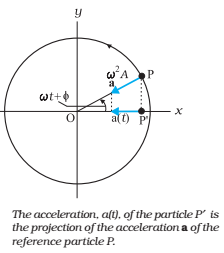
We have seen that a particle executing a uniform circular motion is subjected to a radial acceleration a directed towards the centre. The magnitude of the radial acceleration of P is ω2A. Its projection on the x-axis at any time t is, which is the acceleration of the particle P′ (the projection of particle P).
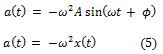
Eq. (5) expresses the acceleration of a particle executing SHM. It is shown that in SHM, the acceleration is proportional to the displacement and is always directed towards the mean position.
![]()
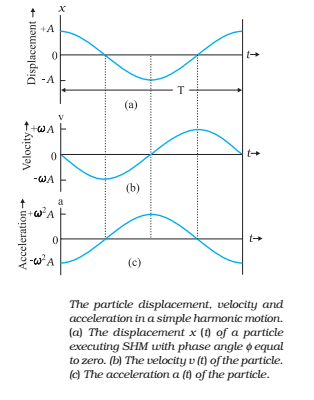
The inter-relationship between the displacement of a particle executing simple harmonic motion, its velocity and acceleration can be seen in below Fig.