The Simple Pendulum
An ideal simple pendulum consists of a point-mass suspended by a flexible, inelastic and weightless string from a rigid support of infinite mass.
In practice, a simple pendulum is obtained by suspending a small metal bob by a long and fine cotton thread about a rigid support.
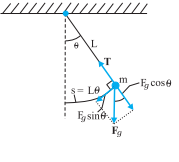
Fig. Force acting on the bob of a pendulum
Expression for time period:
In the equilibrium position, the bob of a simple pendulum lies vertically below the point of suspension. If the bob is slightly displaced on either side and released, it begins to oscillate about the mean position.
- The force acting on the bob is the force T tension in the spring and the gravitational force Fg (mg).
- The string makes an angle θ with the vertical.
- We resolve the force Fg into a radial component Fg cosθ and a tangential component Fg sinθ.
- The radial component is canceled by the tension since there is no motion along the length of the string.
- The tangential component produces a restoring torque about the pendulum’s pivot point. This torque always acts opposite to the displacement of the bob so as to bring it back towards its central location.
- The central location is called the equilibrium position (θ = 0), because at this position the pendulum would be at rest if it were not swinging.
- The restoring torque τ is given by,
![]()
where the negative the negative sign indicates that the torque acts to reduce θ, and L is the length of the moment arm of the force Fg sin θ about the pivot point.
For rotational motion,
![]()
Where I is the pendulum’s rotational inertia about the pivot point and α is its angular acceleration about that point.
Above two equation,
![]()
Substituting the magnitude of Fg i.e. mg, we have,

If we assume that the displacement θ is small. where θ is in radians. So, sinθ can be approx. by θ
![]()
The motion of a simple pendulum swinging through small angles is approximately SHM.
- The angular frequency of the pendulum is,
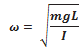
- The period of the pendulum, T, is

All the mass of a simple pendulum is centered in the mass m of the bob, which is at a radius of L from the pivot point. Therefore, for this system, we can write I = mL2
Put it in the equation of time:
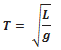
It represents a simple expression for the time period of a simple pendulum.

