Kinetic Theory of Gases

Kinetic Theory of Gases

Assumptions or postulates of the kinetic-molecular theory of gases are given below. These postulates are related to atoms and molecules which cannot be seen, hence it is said to provide a microscopic model of gases.

1. Gases consist of large number of identical particles (atoms or molecules) that are so small and so far apart on the average that the actual volume of the molecules is negligible in comparison to the empty space between them.
2. There is no force of attraction between the particles of a gas at ordinary temperature and pressure.
3. Particles of a gas are always in constant and random motion.
4. Particles of a gas move in all possible directions in straight lines. During their random motion, they collide with each other and with the walls of the container. Pressure is exerted by the gas as a result of collision of the particles with the walls of the container.
5. Collisions of gas molecules are perfectly elastic. This means that total energy of molecules before and after the collision remains same.
6. At any particular time, different particles in the gas have different speeds and hence different kinetic energies.
   It is possible to show that though the individual speeds are changing, the distribution of speeds remains constant at a particular temperature.

If a molecule has variable speed, then it must have a variable kinetic energy. Under these circumstances, we can talk only about average kinetic energy. In kinetic theory it is assumed that average kinetic energy of the
gas molecules is directly proportional to the absolute temperature.

The important mathematical results from this theory are:

K.E. per mole = 3/2 nRT

K.E. per molecule = 3/2 kT

where R = 8.314 and k = R/N_A = 1.38 x 10^-23 J/K

From the above postulates, the kinetic gas equation derived is

pV = 1/3 mn U²

where, U = root mean square velocity

Molecular Distribution of Speeds (Max well Boltzmann Distribution)

The Maxwell Boltzmann Distribution is a plot of fraction of molecules in the gas sample vs. the speed of the gas molecules. The distribution is shown below followed by the salient features of the graph.

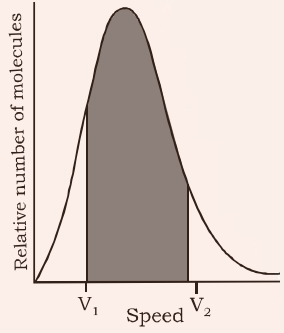
The graph shows that:

• The fraction of molecules having very low or very high speeds is very less.
• Most of the molecules have a speed somewhere in the middle, this is called the most probable speed. (μ_MP)
• The area covered between any two velocities is the number of molecules in that velocity range.
• The total area covered by the graph gives the total number of molecules in the sample and is constant.
• There are two more molecular speeds defined for a sample called average speed (μ_AVG) and root mean square speed (μ_RMS)

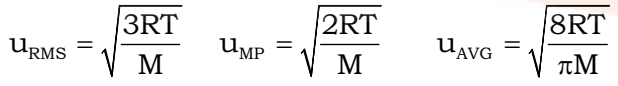
IMP: Always remember to take molecular mass in kg in the above relations.

It’s useful to remember the ratio of μ_MP : μ_AVG : μ_RMS 1:1.128:1.224 for a given gas at the same temperature.